The Perfect Throw: What’s the Best Launch Angle for Maximum Javelin Distance?
Javelin fever has gripped the nation. Every time Neeraj Chopra steps onto the field, millions of Indians freeze—hearts pounding, eyes locked on the screen—waiting for that perfect throw that could etch his name in history once again. I’m one of them.
During the last Olympics, as I watched the javelin event with my brother, I decided to flex my physics knowledge: “For maximum range, javelin throwers should launch at a \( 45^\circ \) angle.” It’s basic projectile motion, right? But throw after throw, the world’s best athletes aimed for 30–35° instead.
I was baffled. These champions train every day, mastering every nuance of their technique—so why weren’t they throwing at the so-called optimal angle? Was everything I thought I knew about physics… wrong?
If you’ve ever wondered the same, buckle up. This article will uncover the real science behind the perfect javelin throw.

You see in case of a javelin the projectile motion principles get tweaked. This is because of three major reasons:
- Height of Release: The Javelin is released from a significant height (6 ft & above). The point of release affects the optimal angle to get the maximum range
- Air Resistance: The javelin is not moving in vacuum (ideal scenario), apart from gravity, air resistance also acts on the javelin
- Turbulence: The javelin is not a point object. It’s elongated body means that javelin will experience the air drag differently than a point object
We will try to find the optimal launch angle for maximum range of the javelin by evaluating these three factors separately and then we will be able to conclude what is the optimal launch angle to get the javelin travel maximum distance.
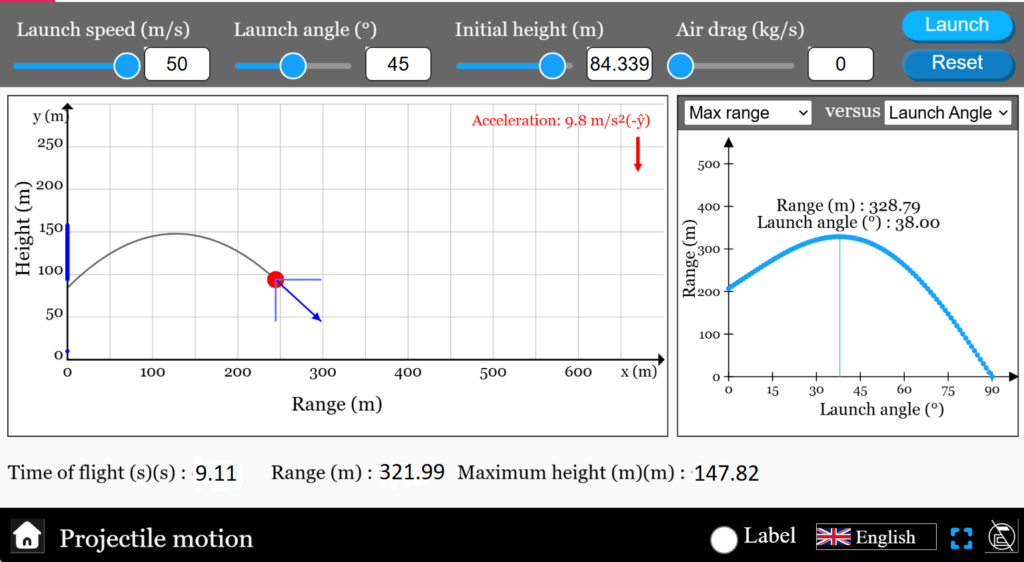
Optimal launch angle for maximum range when projectile is launched from a height h
A projectile is launched from a height \(h\) with an initial velocity \(v_0\) at an angle \(\theta\)
1.1 Horizontal motion when projectile is launched from a height
\begin{equation}
x = v_0 \cos\theta \cdot t
\end{equation}
Since there is no horizontal acceleration, the velocity remains constant.
1.2 Vertical motion when projectile is launched from a height
Using the kinematic equation:
\begin{equation}
y = h + v_0 \sin\theta \cdot t – \frac{1}{2} g t^2
\end{equation}
The projectile reaches the ground when \(y=0\):
\begin{equation}
0 = h + v_0 \sin\theta \cdot t – \frac{1}{2} g t^2
\end{equation}
1.3 Time of flight when projectile is launched from a height
Rearrange the quadratic equation:
\begin{equation}
\frac{1}{2} g T^2 – v_0 \sin\theta \cdot T – h = 0
\end{equation}
Solving for \(T\) using the quadratic formula:
\begin{equation}
T = \frac{v_0 \sin\theta + \sqrt{(v_0 \sin\theta)^2 + 2gh}}{g}
\end{equation}
(Only the positive root is taken, since time cannot be negative.)
1.4 Range
The range is given by:
\begin{equation}
R = v_0 \cos\theta \cdot T
\end{equation}
Substituting \(T\):
\begin{equation}
R = \frac{v_0 \cos\theta \left(v_0 \sin\theta + \sqrt{(v_0 \sin\theta)^2 + 2gh} \right)}{g}
\end{equation}
1.5 Optimal angle for maximum range for a projectile launched from a height
To maximize \(R\) , we differentiate with respect to \(\theta\):
\begin{equation}
\frac{dR}{d\theta} = 0
\end{equation}
Solving this equation analytically is complex, but from physics principles, we find:
- For \(h = 0\) (flat ground), the optimal angle is \(45^\circ\)
- For \(h > 0\), the optimal angle is always less than \(45^\circ\).
- For small \(h\), the correction term gives:
\begin{equation}
\theta_{\text{opt}} \approx \frac{1}{2} \tan^{-1} \left( \frac{2 v_0^2 + 4gh}{g h} \right)
\end{equation}
For significant height, the optimal launch angle decreases further.
\begin{equation}
Optimal range when projectile is impacted by air resistance- ideal scenario
To make case simpler, lets treat the javelin as a point object and then derive its projectile motion. The forces acting on the javelin are:
- Gravity: \( F_g = mg \) (acts downward)
- Air resistance: \( F_r = -k v \) (opposes motion, proportional to speed of projectile).
Using Newton’s second law we will derive the horizontal and vertical motion of the javelin:
2.1 Horizontal motion (x- component) due to air resistance
In horizontal motion, the air resistance acting on the projectile is proportional to the horizontal speed of the projectile and opposes the motion.
\begin{equation}
m \frac{dv_x}{dt} = – k v_x
\end{equation}
Solving the differential equation:
\begin{equation}
v_x = v_{x0} e^{-\frac{k}{m}t}
\end{equation}
Integrating to find position:
\begin{equation}
x = \frac{m}{k} v_{x0} (1 – e^{-\frac{k}{m}t})
\end{equation}
2.2 Vertical motion (y- component) due to air resistance
In vertical motion, two forces act on the motion of projectile. The first being gravity and the second being air resistance that again try to oppose the vertical motion and is proportional to the vertical velocity
\begin{equation}
m \frac{dv_y}{dt} = -mg – k v_y
\end{equation}
Rearranging:
\begin{equation}
\frac{dv_y}{dt} + \frac{k}{m} v_y = -g
\end{equation}
Using an integrating factor \( e^{\frac{k}{m}t} \):
\begin{equation}
v_y = \left(v_{y0} + \frac{mg}{k} \right) e^{-\frac{k}{m}t} – \frac{mg}{k}
\end{equation}
Integrating to find position:
\begin{equation}
y = \frac{m}{k} \left(v_{y0} + \frac{mg}{k} \right) \left(1 – e^{-\frac{k}{m}t} \right) – \frac{mg}{k} t
\end{equation}
2.3 Time of flight due to air resistance
The projectile reaches the ground when \( y = 0 \):
\begin{equation}
\frac{m}{k} \left(v_{y0} + \frac{mg}{k} \right) \left(1 – e^{-\frac{k}{m}T} \right) – \frac{mg}{k} T = 0
\end{equation}
Solving for \(T\):
\begin{equation}
T = \frac{m}{k} \ln \left(1 + \frac{k v_{y0}}{mg} \right)
\end{equation}
Substituting \( v_{y0} = v_0 \sin \theta \):
\begin{equation}
T = \frac{m}{k} \ln \left(1 + \frac{k v_0 \sin \theta}{mg} \right)
\end{equation}
2.4 Range of projectile due to air resistance
The range is given by:
\begin{equation}
R = \int_0^T v_x dt
\end{equation}
Since \( v_x = v_0 \cos \theta e^{-\frac{k}{m}t} \), integrating:
\begin{equation}
R = \frac{m v_0 \cos \theta}{k} \left(1 – e^{-\frac{k}{m} T} \right)
\end{equation}
Substituting \(T\):
\begin{equation}
R = \frac{m v_0 \cos \theta}{k} \left(1 – \frac{1}{1 + \frac{k v_0 \sin \theta}{mg}} \right)
\end{equation}
\begin{equation}
R = \frac{m v_0^2 \cos \theta \sin \theta}{g \left(1 + \frac{k v_0 \sin \theta}{mg} \right)}
\end{equation}
2.5 Finding the Optimal angle \(\theta_{\text{opt}}\) for maximum range
To maximize \( R \), take the derivative:
\begin{equation}
\frac{dR}{d\theta} = 0
\end{equation}
Solving, the optimal angle satisfies:
\begin{equation}
\tan \theta_{\text{opt}} = \frac{1}{1 + \frac{k v_0}{mg}}
\end{equation}
For small air resistance \( (k \to 0) \):
\begin{equation}
\theta_{\text{opt}} \approx 45^\circ
\end{equation}
For higher air resistance:
\begin{equation}
\theta_{\text{opt}} < 45^\circ
\end{equation}
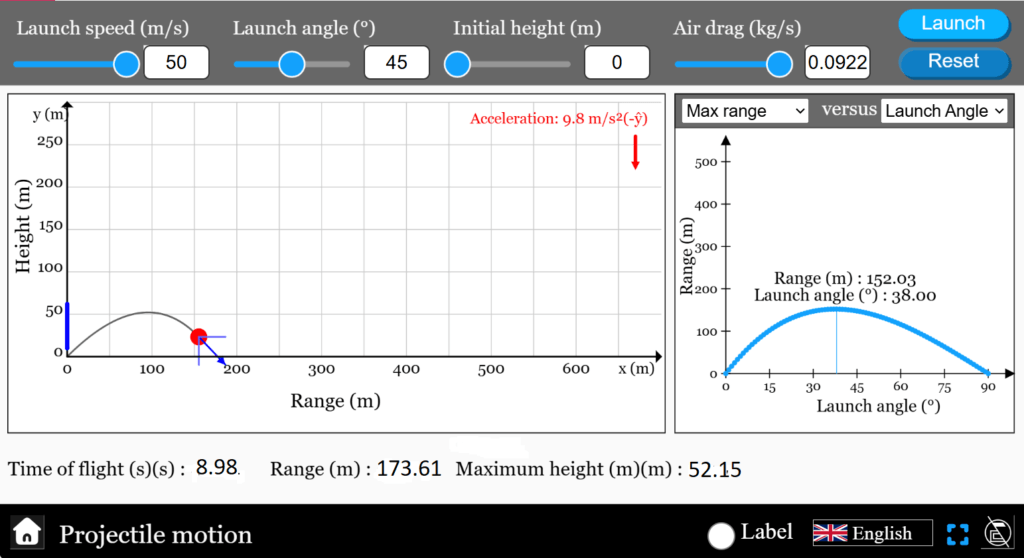
- With air resistance, the optimal launch angle is less than \( 45^\circ \).
- For weak air resistance, \( \theta_{\text{opt}} \approx 40^\circ – 42^\circ \).
- For strong air resistance, \( \theta_{\text{opt}} \approx 30^\circ – 35^\circ \).
Optimal range when projectile is impacted by air resistance -effect of turbulence
In the previous case we treated javelin as a point object. But in real life, javelins are long cylindrical projectiles. Thus javelins will experience air drag differently . To understand the air drag, we have to introduce the Reynolds number (Re), a key parameter in fluid dynamics that helps classify different drag regimes.
The Reynolds number (Re) is given by:
\begin{equation}
\text{Re} = \frac{\rho v L}{\mu}
\end{equation}
where:
- \( \rho \) = air density (\(kg/m^3\))
- \(v\) = velocity of the projectile (\(m/s\))
- \(L\) = characteristic length (e.g., diameter of a javelin or ball)
- \( \mu \) = dynamic viscosity of air (\(Pa·s\))
The Reynolds number determines the drag behavior:
-
Low Re (Re<1000) – Viscous (Laminar) Flow: Laminar flow, drag proportional to velocity (\(F_{\text{drag}} \propto v\)).
- High Re ( Re > \( 10^4)\): Turbulent flow, drag follows quadratic relation (\(F_{\text{drag}} \propto v^2\))
In case of a javelin, the Reynolds number is high due to its length and high speed of launch. Hence the javelin experiences quadratic air-drag.
Due to the stronger air drag, the javelin spends lesser time in air than a point object. Similar to previous scenario (treating the javelin as a point object), the optimal angle shifts below \( 45^\circ \) . For the fast moving javelins, the air drag is higher and this results in greater reduction in optimal launch angle.
Conclusion
- Due to height of launch, air resistance and length, the optimal launch angle for a javelin is \( \theta_{\text{opt}} \approx 30^\circ – 35^\circ \).
- This is the reason why javelin throwers launch their javelin at an angle of \( \theta \approx 30^\circ – 35^\circ \)



